Professor Steven J. Brams developed a general dynamic modeling framework called the “Theory of Moves” (or TOM) and used it to offer several (plausible) explanations of the 1962 Cuban Missile Crisis.
By Frank C. Zagare
Professor
Steven J. Brams developed a general dynamic modeling framework called the
“Theory of Moves” (or TOM) and used it to offer several (plausible)
explanations of the 1962 Cuban Missile Crisis. Brams [1] also developed a few
explanations using standard game-theoretic concepts. For instance, he suggests
that the compromise outcome can also be supported in equilibrium if Khrushchev
either deceived the United States by suggesting that the compromise outcome was
his most-preferred (when it was not) or if his preferences “deteriorated” as
the crisis progressed and the compromise outcome actually was his
most-preferred. Additionally, Brams constructed an extensive-form game model in
which the compromise outcome is a (sub-game perfect) Nash equilibrium.
In this
article, we will concentrate on the theoretical core of all his explanations
and ignore the subtle differences that set the various explanations apart. Like
Fraser and Hipel [2], Brams abandons both a normal-form representation and the
standard Chicken analogy. Instead he begins by considering the “payoff matrix”
given by Figure 1.
Figure 1: The Cuban
Missile as seen by Brams [1]
The cells of
this graphical summary of the crisis represent possible states of the world (or
outcomes). The ordered pair in each cell of the matrix reflects Brams’
understanding of the relative ranking of the four possible outcomes by the
United States and the Soviet Union, respectively. Brams assumes that once a
game begins either player can move from whatever outcome is the initial state
(or status quo outcome) and, if it does, the other can respond, the first can
counter-respond, and so on. The process continues until one player decides not
to respond, and the outcome that they are at is the final outcome. Any outcome
from which neither player, looking ahead indefinitely, has an incentive to move
to another state of the world, including the initial state, is said to be a
nonmyopic equilibrium.
When Kennedy announced the blockade on October 22, the Soviet missiles were already being installed in Cuba. This, the initial state of the world, was the worst for the United States and best for the Soviet Union. Thus this outcome is labeled “Soviet Victory”. Brams [1] suggests several reasons why the Soviet Union would then withdraw the missiles and induce its next-best outcome, the Compromise outcome, rather than stick with its initial choice. For example, if the United States had what he calls moving power, which is the ability to continue moving in a game when the other player cannot, it could induce the Soviet Union to end the game at (3,3) by forcing it to choose between (3,3) and (4,1). Or, if the United States possessed threat power, which is the ability to threaten a mutually disadvantageous outcome in the first play of a repeated game, it could similarly induce the Soviet Union to withdraw the missiles by threatening to remove them with an air strike if they did not.
But regardless of the reason why the Soviets decided to withdraw the missiles, once they did, the game ended. Brams’ explanation [Superpower Games; Yale University Press] is that the Compromise outcome is a nonmyopic equilibrium, that is, neither player can do better by moving the game to another state of the world by changing its strategy choice, given that the other might then switch to another strategy, it might then be forced to also change its strategy, and so on.
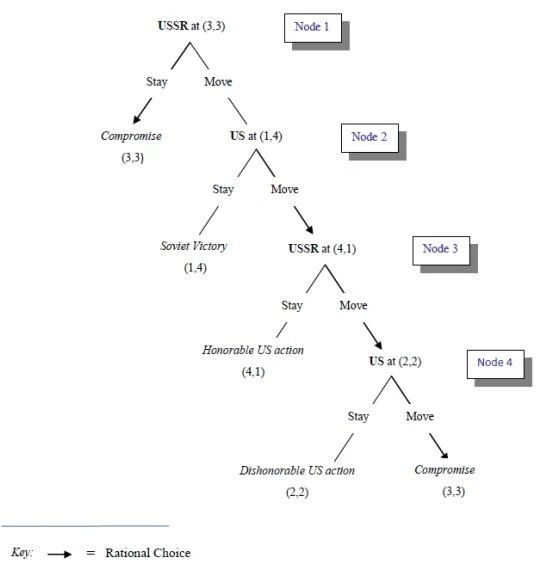
To see this,
consider Figure 2 which lists the sequence of moves and countermoves away from
the Compromise outcome that would be touched off if the Soviet Union reversed
its course and decided to maintain the missiles after all. At the last node of
this tree, the United States has a choice of staying at its second-worst
outcome or cycling back to the Compromise outcome, its second-best. As
indicated by the arrow, the United States would rationally move.
Figure 2: Moves and
Countermoves during the Cuban Missile Crisis, starting with the Soviet Union at
the Compromise Outcome (3,3)
Similarly, at the previous node, the Soviet Union would move away from (4,1) its least-preferred outcome to its next-worst outcome (2,2). But it would do so not because it prefers (2,2) to (4,1)— which it does—but because it would anticipate the outcome induced by the American choice at the subsequent node which is better still. Counter-intuitively, perhaps, the United States would, at the second node of the tree, also rationally move to its best outcome, not because it is its best outcome, but because it prefers to cycle back to the Compromise outcome, which is its second-best, to terminating the game at (1,4), its least-preferred outcome.
Finally, Brams argues that the Soviet Union would stick with its choice (at the top of the tree) to withdraw the missiles simply because, by not doing so, it would only cycle back to the Compromise outcome. As Brams [3] asks, “what is the point of initiating the move-countermove process if play simply returns to ‘square one’?”
It would be a
straightforward exercise to show that there is also no incentive for the United
States to precipitate the move-countermove process once the Compromise outcome
is reached. And since neither player has a long-term incentive to move away
from this outcome if and when it is reached, it constitutes a nonmyopic
equilibrium.
Brams’
explanation proceeds from this fact. As in the equilibrium, the Compromise
outcome is, by definition, consistent with the rationality postulate. And since
it is the only non-myopic equilibrium in the matrix of Figure 4, it is the only
outcome that can persist under rational play. All of which is another way of
saying that the Soviet Union withdrew the missiles because, looking ahead, they
believed that maintaining them would not be in their long-term interest. Given
the American blockade and the incentive structure of the game, they simply
could not win.
There is
obviously much to like about the Theory of Moves framework. Indeed, I have used
it myself to explore the dynamics of both one-sided and two-sided deterrence
relationships and to analyze a number of acute interstate crises (Zagare,
[4]). The Theory of Moves is a simple and extremely intuitive methodology for
analyzing complex interstate conflicts like the missile crisis; it is also more
general than the analysis of options technique developed by Fraser and Hipel
[2]; its major solution concepts are easy to calculate and interpret; and
since it is based only on ordinal utilities, it requires fewer “heroic
assumptions” than many other game-theoretic frameworks.
In the case of
the missile crisis, however, its strengths are also it weaknesses. Since the
concept of a nonmyopic equilibrium has not as yet been successfully defined in
games in which the players have more than two strategies each, it can only be
used to assess the rationality of four outcomes at a time. This limitation
explains why Brams starts his analysis on October 22, the day that Kennedy
announced the blockade. In consequence its theoretical range is restricted. Why
did the Soviets precipitate the crisis by installing the missiles in the first
place and why did the United States then respond by blockading Cuba? These are
questions that Brams does not address and, in fact, cannot address within the
confines of a single integrated game model using the Theory of Moves framework.
Thus, while his analysis of the end-game of the crisis is both insightful and
penetrating, his explanation remains incomplete.
About Professor Steven J. Brams
Professor Steven J. Brams is a game theorist and political scientist at
the New York University Department of Politics. Brams is best known for using
the techniques of game theory, public choice theory, and social choice theory
to analyze voting systems and fair division. He is one of the independent discoverers
of approval voting, as well as an extension of approval voting to
multiple-winner elections known as Satisfaction approval voting.
Fellowships/Honors: American
Association for the Advancement of Science Fellow, 1992; President, Peace
Science Society, 1990-1991; Guggenheim Fellow, 1986-1987; Russell Sage
Foundation Visiting Scholar, 1998-1999, President, Public Choice Society,
2004-2006 (Fellow, 1998).
External
Affiliations: American Political Science Association, International
Studies Association, Peace Science Society, Public Choice Society, Social
Choice and Welfare Society, American Association for Advancement of Science.
About The
Author:
Frank C.Zagare is UB Distinguished Professor of Political Science. A former Vice
President of the International Studies Association, Dr. Zagare is a member of
the editorial board of International Interactions. He has served on the
Advisory Panel of the National Science Foundation, on the editorial board of
International Studies Quarterly, as a member of the Presidential Nominating
Committee and the Professional Rights and Responsibilities Committee of the
International Studies Association, as a Councilor for the Peace Science Society
(International), as a Council Member of the Conflict Processes Section of the
American Political Science Association. In
2005 he received the Susan Strange Award from the International Studies
Association. He is the author, co-author or editor of six books including
Perfect Deterrence (with D. Marc Kilgour), The Dynamics of Deterrence, and Game
Theory: Concepts and Applications.
Publication
Details:
This article is an extract from a paper titled -“A Game-Theoretic History of the Cuban Missile
Crisis by Frank C. Zagare” economies ISSN 2227-7099 www.mdpi.com/journal/economies/
doi:10.3390/economies2010020, published under Creative Commons License. Download The Paper - LINK
References:
[1] Brams, S.J. Superpower Games; Yale University Press: New Haven, CT, USA, 1985
[2] Fraser, N.M.;
Hipel, K.W. Dynamic modelling of the Cuban missile crisis. Confl. Manag. Peace
Sci. 1982, 6, 1–18.
[3] Brams, S.J. Game Theory and the Cuban Missile Crisis. Available online: http://plus.maths.org/
content/os/issue13/features/brams/index
[4] Zagare, F.C.
The Dynamics of Deterrence; University of Chicago Press: Chicago, IL, USA, 1987